Years back, I encountered the following problem in a book on Number Theory: Prove that the sum \(H_n = 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}\) is never an integer after \(n > 1\). In other words, in the sequence \(1, 1+\frac{1}{2}, 1+\frac{1}{2}+\frac{1}{3}, \dots\), there is only one integer, and that is the first number \(1\).
Even though I had some vague ideas for a proof, it took me quite a long time to actually prove the statement. Of course, this has more to do with my own inability than with the hardness of the problem itself. As it turns out, the problem is not that difficult.
First of all, let us understand that when the problem talks about integers, it means real, exact integers. Not approximations like \(1.000\dots0001\) or \(3.99999999\dots\). So when it says that the sequence \(H_n\) is never an integer for \(n>1\), it means that the sum is never a fraction where the numerator is an exact multiple of the denominator.
Let us also remind ourselves that in order for two simplified fractions (where the numerator and the denominator have no common factors other than 1) to add up to an integer, both should have the same denominator. Convince yourself that this is indeed the case.
It always helps to see some examples to get an idea about what we need to prove. We can manually compute the fractions, but why bother, when we can write a script to do it? The good thing is that Python comes with a library called fractions for manipulating rational numbers, so we don’t have to worry about writing code for adding or simplifying fractions. Here is the function:
from fractions import Fraction
def harmonic(n):
s = 0
sum_fs = []
for i in range(1, n+1):
s += Fraction(1, i)
sum_fs.append(s)
return sum_fsWhen called with \(n=5\), the function tells us that the first \(5\) harmonic numbers are \(1, \frac{3}{2}, \frac{11}{6}, \frac{25}{12}\), and \(\frac{137}{60}\). Now think about what it takes to turn each of the numbers to an integer. We need to add a fraction with denominator \(2\) to make \(H_2\) an integer. Similarly, \(H_3\) needs a denominator of \(6\), \(H_4\) needs a \(12\) and \(H_5\) needs a \(60\). Note that the respective denominators are not sufficient \(–\) they are just necessary. For example, we can add \(\frac{5}{6}\) to \(H_3\) and the resulting fraction, \(\frac{8}{3}\), is not an integer. But any number \(r\) such that \(H_3 + r\) is an integer should have the denominator \(6\).
So what can we infer from the first five Harmonic numbers? The denominators appear to be increasing. In fact they seem to be increasing much faster than the natural numbers. Could we utilize this property to prove the claim? If we could show that the denominators are monotonously increasing, and that they are increasing at a higher rate than the indices \(n\), we could conclude that at no point after \(n > 1\), we would have \(H_n + \frac{1}{n+1}\) as an integer. This is because to be an integer, \(H_n\) requires a fraction with denominator far greater than \(\frac{1}{n+1}\). Let us gather more data to boost this idea. Let us compute the first \(10\) harmonic numbers. \(1, \frac{3}{2}, \frac{11}{6}, \frac{25}{12}, \frac{137}{60}, \frac{49}{20}, \frac{363}{140}, \frac{761}{280}, \frac{7129}{2520}\), and \(\frac{7381}{2520}\).
Darn! The denominators are not monotonously increasing! That’s a shame. What can we do? Should we scrap the whole idea or can we use it in another way? Maybe there is something about the denominators that is monotonously increasing, even though the denominators themselves are not. Let us take a break and think about it!
OK, the idea that seems to work is related to the great little number \(2\). Check out the maximum power of \(2\)’s in the denominators of \(H_n\). Again, we can do it manually. But then again, we could be lazy and write a function to do that.
def max_power_two(n):
s = 1
while n % 2 == 0:
s *= 2
n //= 2
return sThat //, btw, is the Python 3 integer division operator (as opposed to /, the floating point division operator).
Using the following snippet, we can compute the largest power of \(2\) which divides the denominators of the first \(10\) harmonic numbers:
[max_power_two(fr.denominator) for fr in harmonic(10)]And the numbers are \(1, 2, 2, 4, 4, 4, 4, 8, 8\), and \(8\). Things start to look promising! Is there a pattern here? \(H_2\) requires a fraction whose denominator is a multiple of \(2\). So does \(H_3\). \(H_4\) is hungrier \(–\) it wants one more two. So do \(H_5, H_6\), and \(H_7\). \(H_8\) becomes hungrier again, and so on. We seem definitely to be onto something here. If we can actually prove that this trend continues, we would be on a home run. I urge you to think about it for some time before moving on.
Here is an informal argument as to why this trend holds up. Let us take the concrete example of \(H_4\). Its denominator is \(12\). So we need to add a fraction with a denominator which is a multiple of \(4\) (specifically, \(12\)) in order to make the sum an integer. Now \(H_5\) is \(H_4 + \frac{1}{5}\), and as \(5\) is an odd number, we know that the denominator of the sum would still have exactly the same factor of \(4\). The next harmonic number is more interesting. \(H_6\) is \(H_5 + \frac{1}{6}\). Could the denominator of the sum contain less \(2\)’s than \(H_5\)? No, that is impossible. As this is a crucial point, we will make a general argument: If we add \(\frac{a}{2^i b}\) and \(\frac{c}{2^j d}\), with \(i
j\) and \(a, b, c, d\) odd numbers, we would get \[ \frac{ad+2^{i-j}bc}{2^i bd}\] Note that the numerator is still odd, and the denominator still contains exactly \(i\) \(2\)’s. That is, the number of \(2\)’s in the denominator becomes the maximum of \(i\) and \(j\). This happens whenever \(i\) and \(j\) are different (What happens when \(i = j\)?). In our particular case, it implies that the denominator \(H_6\) would be a multiple of \(4\).
By the same argument, \(H_7\) would also have a multiple of \(4\) in the denominator. Now comes the next crucial case, \(H_8\). \(H_{8}\) is the sum of \(H_7\) and \(\frac{1}{8}\). \(H_7\) has a \(4\)’s multiple and \(H_8\) has an \(8\)’s multiple in their respective denominators. What happens to the sum? This is exactly like the case of \(H_6\), but in reverse. By our general argument with \(i=3\) and \(j=2\), we can predict that the sum’s denominator would have \(8\) as a factor.
You probably see the pattern now. Since \(H_4\) contains \(4\) in the denominator, to make it an integer we need to add a fraction whose denominator is also a multiple of \(4\). Unfortunately, in the case of the harmonic series, the next such number is \(\frac{1}{8}\), and this number, instead of eliminating the existing \(4\), provides one more \(2\). And the saga continues. In general, if \(H_{2^m}\)’s denominator contains \(2^m\), \(H_{2^{m+1}}\)’s denominator would contain \(2^{m+1}\). This, along with the fact that the denominator of \(H_{2^0}\) (\(=H_1\)) has \(2^0\) (\(=1\)) as a factor, allows us to conclude the original claim by the principle of mathematical induction.
For confirmation, let us see a graph of \(n\) vs the largest power of \(2\) in the denominator of \(H_n\).
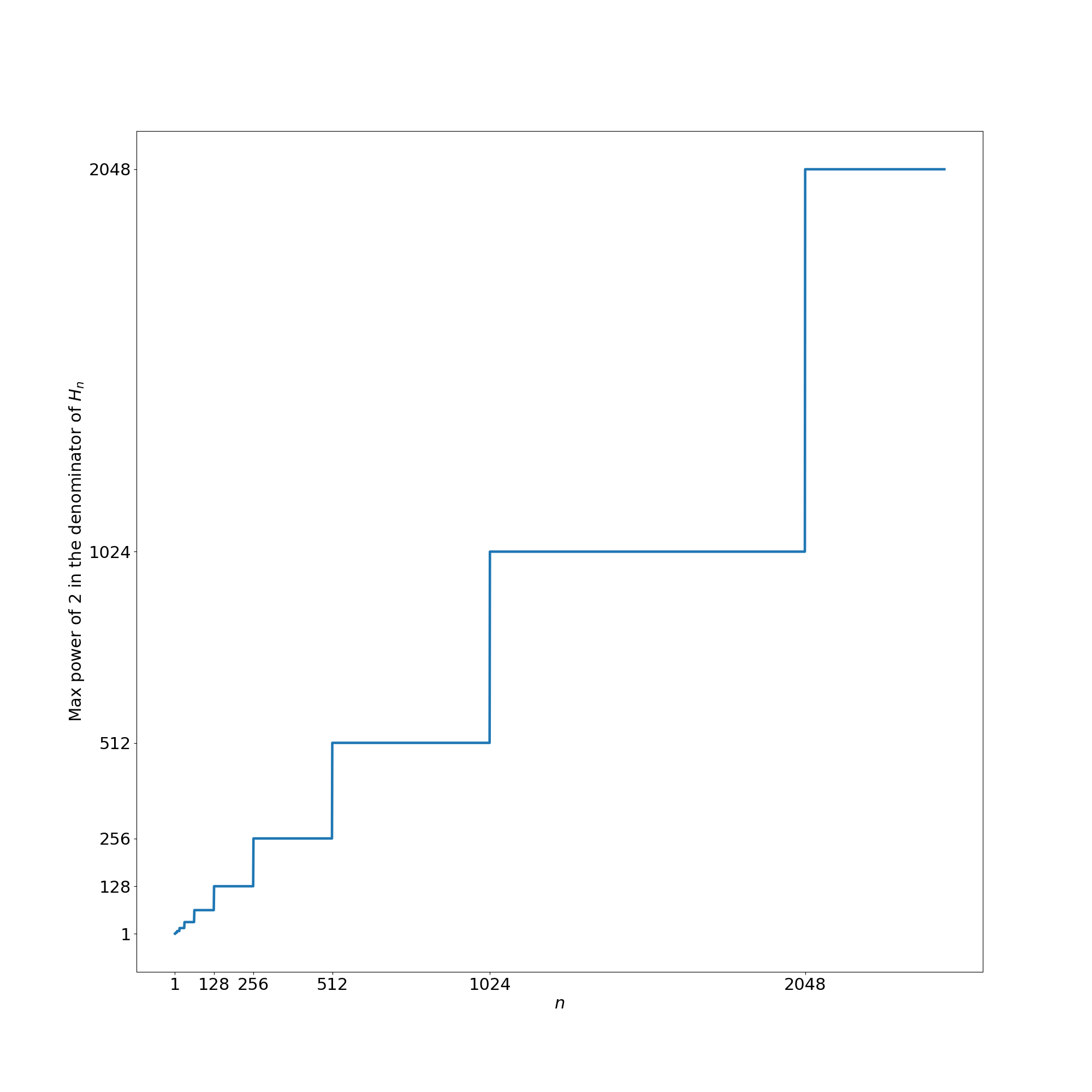
As expected, the graph is a nice step function.
As a more powerful check, we can automatically verify, for a large number of integers \(m\), that the maximum power of \(2\) in the denominator of \(H_m\) is indeed the maximum power of \(2\) that is less than or equal to \(m\). The following code does that.
def harmonic_power_two_check(n):
max_twos = [max_power_two(fr.denominator) for fr in harmonic(n)]
cur_power_two = 2
last_i = 1
while cur_power_two <= n:
for i in range(last_i, cur_power_two):
if max_twos[i-1] > cur_power_two:
print("Your proof is bunkum! Counter example at i = {0}, s = {1}".format(i, cur_power_two))
return
last_i = cur_power_two
cur_power_two *= 2
print("No counter-example found!")The code basically checks that the denominators of all harmonic numbers from \(H_{2^i}\) until \(H_{2^{i+1}-1}\) have exactly \(2^i\) as the maximum power-of-\(2\) factor. When I ran the code for \(n = 100000\), my laptop almost got fried, but at the end of 15 or so minutes, I got the following output:
No counter-example found!
Whew! That’s a relief!